Zeit zum Spielen - Sudokutrainer

Sudoku ist ein beliebtes Spiel und sehr gut geeignet, seine grauen Zellen in Schuss zu halten. Und sei es nur für ein paar Minuten im Autobus oder in der Bahn auf dem Weg in die Arbeit.
Für Neulinge stellt sich oft die Frage, wie löst man so etwas?
Ist die Aufgabe, die ich gerade in einer Zeitung oder Zeitschrift gefunden habe, überhaupt lösbar und wenn ja wie?
Welche Strategien gibt es dabei?

Gleichzeitig ist die Aufgabenstellung der Lösungsfindung und der Visualisierung des Lösungsansatzes ein hervorrangendes Beispiel, um Software-Konzepte in neuen Umgebungen bzw. in verschiedenen Programmiersprachen auszuprobieren. Daher habe ich diese Aufgabenstellung in einer reinen Weblösung (mit HTML/CSS/Javascript) implementiert, sodaß sie jeder einfach über seinen Browser verwenden kann. Sobald die Seite geladen ist, ist auch keine weitere Internetverbindung mehr notwendig (d.h. funktioniert auch in Umgebungen mit schlechter Internet-Verbindung, falls es so etwas heute noch gibt ;-) )

Viel Spass mit dem Sudokutrainer

Hier noch eine kurze Erklärung zu den Steuerungselementen und den Lösungsstrategien.

Sudokutrainer

Layout

Je nach verwendetem Browser bzw. zur Verfügung stehender Darstellungsfläche gibt es 2 Darstellungsvarianten, in denen die Bedienelemente unterschiedlich angeordnet werden

Landscape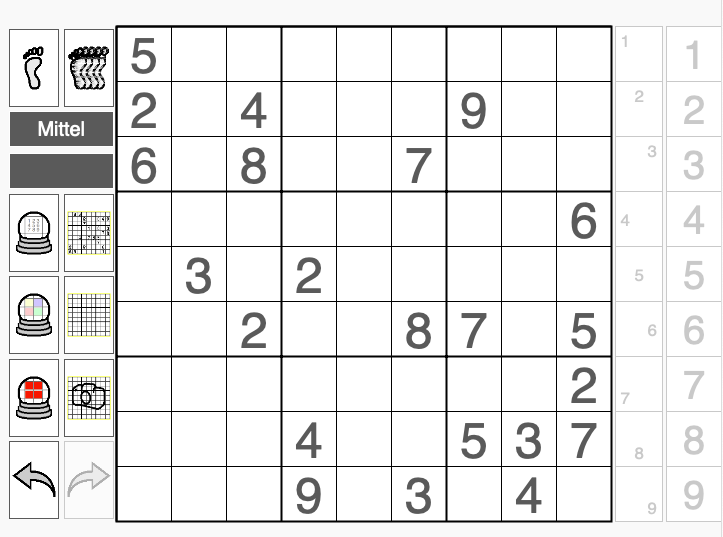

Portrait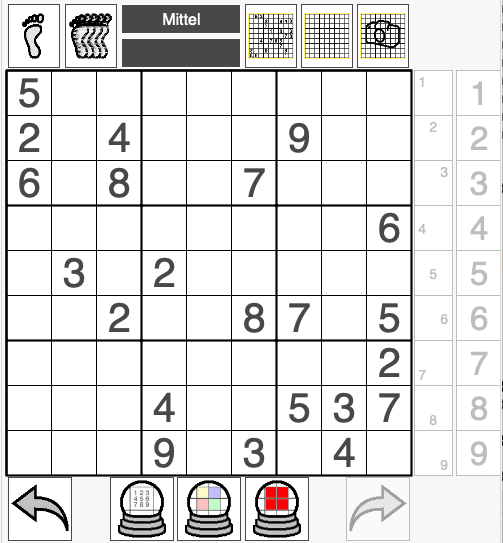

Spiel erzeugen

Mit (bzw. Ctrl-G) kann ein neues Spiel mit zufälliger Schwierigkeit erzeugt werden

Mit (bzw. Ctrl-E) wird das Spiel geleert, keines der Felder ist mit einer Zahl belegt.
Dies eignet sich hervorragend, um vorhandene Aufgabenstellungen (z.B. aus Zeitungen) einzugeben und den Lösungsweg dafür zu lernen.

Ergebnisse setzen bzw. Zahlen notieren

Durch Click auf die Zelle oder mit den Cursor-Tasten kann der Cursor bewegt werden. Durch Eingabe einer Zahl (1-9) wird diese als Lösungszahl gesetzt, bei Eingabe von 0 wird die Zelle geleert. Durch Eingabe einer Zahl (1-9) plus Ctrl/Strg-Taste wird eine Zahl vorgemerkt.

Lösung automatisch finden

Mit kann der nächste optimale Lösungsschritt automatisch durchgeführt werden (siehe Strategien)

Mit kann die Aufgabenstellung vollständig gelöst werden.
Dies macht aber keine Spass, und daher wird das sehr selten verwendet :-)

Undo/Redo

Um die letzten Aktionen wieder rückgängig zu machen, kann (bzw. Ctrl-Z) verwendet werden. Um die rückgängig gemachten Aktionen neuerlich durzuführen, steht (bzw. Ctrl-Y) zur Verfügung.

Lösungshinweise anzeigen

Eine häufige Vorgangsweise bei der Lösung ist, sich die noch möglichen Zahlen in der Zelle zu notieren und entsprechend zu streichen, wenn andere Zellen gelöst wurden. Mit können alle noch möglichen Zahlen automatisch dargestellt werden.

Um Lösungsstrategien zu lernen, kann durch Aktivierung von die für diese Zelle aktuell beste Lösungsstrategie farblich dargestellt werden. Bei gleichzeitger Aktivierung von werden die dargestellten Zahlen auch entspr. der Strategien reduziert (z.B. bei Equivalenzklassen)

Um festzustellen, ob ein aktueller Zustand auch tatsächlich zu einer eindeutigen Lösung führt, kann verwendet werden. Dies empfiehlt sich, um Irrwege zu ersparen, gleichzeitig aber auf die obigen Hinweise zu verzichten.

Lösungsstrategien

Nur noch ein Wert in der Zelle möglich: wenn man die noch möglichen Werte einer Zelle betrachtet, so steht nur mehr genau ein einziger Wert zur Verfügung.
Dies ist die einfachste Strategie, die mit dargestellt wird
Ein Wert ist nur mehr in einer Zelle eines Bereiches (Zeile, Spalte, Quadrat) möglich In der Zelle selbst sind noch mehrere Zahlen möglich. Eine dieser Zahlen ist aber nur mehr in dieser Zelle und keiner anderen Zelle in der Zeile, Spalte ODER im Quadrat möglich.
Darstellung mittels
Durch Ausschluss anderer Zahlen in Equivalenzklassen, ist nur mehr eine Zahl möglich In der Zelle selbst sind noch mehrere Zahlen möglich. In einer Gruppe von Zellen in einem der Bereich sind aber nur mehr genau so viele Zahlen möglich als Anzahl Zellen. Damit können diese Zahlen in keinen anderen Zellen mehr vorkommen und können dort ausgeschlossen werden. Darstellung mittels
Ein Beispiel zur Veranschaulichung: Wenn in 3 Zellen eines Bereiches nur mehr "1,4","1,9" u. "4,9" möglich sind, so müssen diese Zahlen in diesen 3 Zellen verwendet werden und können in allen anderen des jeweiligen Bereiches ausgeschlossen werden. Diese Zellen bilden eine Equivalenzklasse, die in anderen ausgeschlossen wird.
Durch rekursiven Ausschluss anderer Zahlen in Equivalenzklassen, ist nur mehr eine Zahl möglich Wird das Verfahren aus Strategie 3 rekursiv angewendet, so kann es vorkommen, dass erst nach mehr als einem Schritt eine eindeutige Lösung identifiziert werden kann. Diese wird mittels dargestellt.
Forwardchecking/Backtracking Falls keine der obigen Strategien für eine der noch offenen Zellen zur Verfügung steht, kann nur ein Forwardchecking ("wir versuchen, ob wir mit einer zufälligen Lösung ans Ziel kommen") und im Fehlerfall ein Zurücknehmen aller Entscheidungen bis dahin (Backtracking) zur vollständigen Lösung führen. Diese Zellen, werden weiss dargestellt. Diese Strategie ist natürlich nur dann einzusetzen, wenn für alle anderen Zellen keine bessere Strategie mehr zur Verfügung steht.